今回は、「交流電圧の平均値の求め方(三角波編)」についての説明です。
周期T[s]の交流電圧v(t)の平均値Vavは、以下のように定義されています。
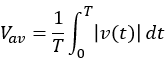
交流電圧の平均値の定義式
周期T[s]の交流電圧v(t)の平均値Vavは、以下のように定義されています。
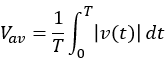
この定義式は、交流電圧の絶対値を0~Tの範囲(1周期)で積分し、周期Tで割ることで平均値が導き出されるという意味です。
つまり、T[s]当たりに計何[V]の電圧がかかるかを求めて、その値を周期Tで割ることで1[s]当たりの電圧を導き出そうとしているわけです。
だからこの定義式で平均値が求まるのです。
※ 交流は極性が変化するので、定義式には絶対値が付いています。
三角波交流の平均値の求め方
定義式を使って正弦波の平均値を実際に求めてみます。
…まあ、計算するまでもなく図を見ればわかるでしょうけどね。
定義式に当て嵌めると計算で求めることができるという確認のためにやってみます。
図1左のような振幅Vm[V]の三角波交流があります。
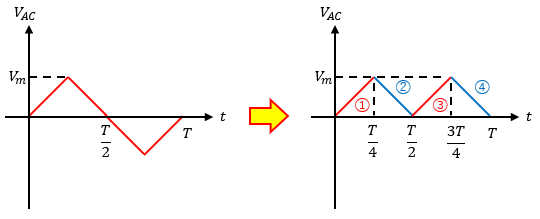
この三角波を式で表そうとすると、正弦波のように一つの式で表すことができません。
なので、部分部分で切り取って考えていく必要があります。
絶対値が付いていることからもわかる通り、平均値を求めるには符号をプラスに統一する必要があるので、図1右のように変形します。
ここで、①~④の傾きと切片を求めて、一次関数で表します。
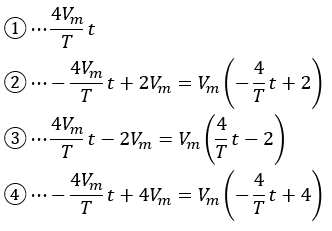
この式を、それぞれ積分していきます。
積分範囲は図1から読み取りましょう。

これで三角波の平均値を求めることができました。
正弦波交流の平均値と言えば2Vm/πですが、あれは交流全体の平均値ではなく、あくまで”正弦波の”平均値だという点には注意しましょうね。
以上、「交流電圧の平均値の求め方(三角波編)」についての説明でした。
【基礎から学ぶ交流回路】
◎直流と交流の違い ~極性が変わらなければ交流ではない
◎正弦波交流 ~正弦波の周期と周波数
◎正弦波交流の位相のズレ
◎正弦波交流の平均値と実効値
◎交流電圧の平均値の求め方 ~正弦波編
◎交流電圧の実効値の求め方 ~正弦波編
◎交流電圧の平均値の求め方 ~三角波編
◎交流電圧の実効値の求め方 ~三角波編
◎整流形計器の平均値と実効値
◎正弦波交流のベクトル表示・フェザー表示
◎交流回路のオームの法則
◎交流電流の位相の変化 ~リアクタンス成分は位相がπ/2ズレる
◎R-L-C直列回路のポイント ~インピーダンスの三角形を描け!
◎R-L-C並列回路のポイント ~電流の三角形を描け!
◎交流回路の共振 ~直列共振と並列共振について
◎R-L-C直並列回路の共振
◎交流回路の電力 ~位相差による力率という考え方
◎交流回路のインピーダンスと電力の関係
◎交流回路のインピーダンスの複素数表示
◎交流回路の電力の複素数表示
◎交流ブリッジ回路と平衡条件
◎過渡現象と時定数
◎R-L-C直並列回路の定常状態の考え方
◎ひずみ波 ~基本波・高調波とは?
◎ひずみ波の消費電力 ~抵抗で消費される平均電力の求め方
◎変調 ~ひずみ波の使われ方とAM変調度の求め方
◎復調 ~ひずみ波から特定の周波数を取り出す方法
