今回は、「直流と交流の違い」についての説明です。
初めに
電気には直流と交流という2つの種類があります。
なんとなく直流は一定の電流・電圧、交流は正弦波状に変化する電流・電圧と思っている方は多いのではないでしょうか?
実は、この認識は間違えています。
今回は、そんな直流と交流の違いについてまとめていきます。
直流とは?
直流はDCと表示されていることがあります。
DCとは、[Direct Current]の略称です。
そのまま直訳で[直流]となるわけです。
電圧を表現する時にDC24VとかDC5Vなどの表示を見たことがあるかと思います。
アレのことです。
では、直流とは何なのかというと、正負の符号が変化しない電流または電圧のことです。
直流の例は乾電池です。
乾電池ってはめ込む方向が指定されていますよね?
あれは、直流はプラス/マイナスの符号が決まっているので、決まった方向にしか電流が流れないようになっているからです。
だから反対にはめ込むと電流が流れなくて動かないんですね。
交流とは?
交流はACと表示されていることがあります。
ACとは、[Alternating Current]の略称です。
そのまま直訳で[交流]となるわけです。
電圧を表現する時にAC100VとかAC200Vなどの表示を見たことがあるかと思います。
アレのことです。
では、交流とは何なのかというと、時間経過で周期的に大きさ及び正負の符号が変化する電流または電圧のことです。
例えば、図1のような正弦波は交流にあたります。
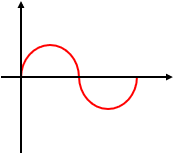
交流は変電所から家庭用コンセントに供給されています。
コンセントって特に挿す向きに指定が無いですよね?
あれは、交流はプラスになったりマイナスになったりと変化するものだから、それを前提に設計された電気機器/電子機器に繋いでいるためです。
どちら向きに挿し込もうが関係ないのです。
一応向きはあるんですけどね。
直流と交流の違い
さて、直流は「正負の符号が変化しない電流または電圧」、交流は「時間経過で周期的に大きさ及び正負の符号が変化する電流または電圧」と述べました。
つまり、直流と交流では以下のような違いがあると言えます。
| 直流 | 交流 | |
|---|---|---|
| 極性 | 変化しない | 変化する |
| 周期性 | あっても良い | ある |
| 大きさ | 変化しても良い | 変化する |
これだけ見てもイメージはしづらいので、いくつか例を見てみましょう。
図1のような正弦波を振り返ってみましょう。
これは交流です。
極性が周期的に変化していているのでまごうこと無き交流です。
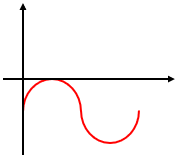
図2のような正弦波があります。
これは直流です。
大きさは変化しています。
また、周期性もあります。
この時点では実は直流と交流の条件をどちらも満たしています。
ですが、極性はプラスとマイナスを行ったり来たりしているでしょうか?
していませんよね。
ということで、これは交流ではなく直流なのです。
直流というと直線になっているイメージを持っているかもしれませんが、実際のところはそんなことはないんですよ。
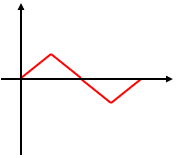
図3のような三角波があります。
これは交流です。
大きさが変化していて、周期性があり、極性も変化していますので、交流の条件を満たしていますからね。
このように、正弦波だから交流などの決まりはなく、あくまで直流は「正負の符号が変化しない電流または電圧」、交流は「時間経過で周期的に大きさ及び正負の符号が変化する電流または電圧」を満たしている波形を指しています。
間違えないように注意しましょうね。
以上、「直流と交流の違い」についての説明でした。
【基礎から学ぶ交流回路】
◎直流と交流の違い ~極性が変わらなければ交流ではない
◎正弦波交流 ~正弦波の周期と周波数
◎正弦波交流の位相のズレ
◎正弦波交流の平均値と実効値
◎交流電圧の平均値の求め方 ~正弦波編
◎交流電圧の実効値の求め方 ~正弦波編
◎交流電圧の平均値の求め方 ~三角波編
◎交流電圧の実効値の求め方 ~三角波編
◎整流形計器の平均値と実効値
◎正弦波交流のベクトル表示・フェザー表示
◎交流回路のオームの法則
◎交流電流の位相の変化 ~リアクタンス成分は位相がπ/2ズレる
◎R-L-C直列回路のポイント ~インピーダンスの三角形を描け!
◎R-L-C並列回路のポイント ~電流の三角形を描け!
◎交流回路の共振 ~直列共振と並列共振について
◎R-L-C直並列回路の共振
◎交流回路の電力 ~位相差による力率という考え方
◎交流回路のインピーダンスと電力の関係
◎交流回路のインピーダンスの複素数表示
◎交流回路の電力の複素数表示
◎交流ブリッジ回路と平衡条件
◎過渡現象と時定数
◎R-L-C直並列回路の定常状態の考え方
◎ひずみ波 ~基本波・高調波とは?
◎ひずみ波の消費電力 ~抵抗で消費される平均電力の求め方
◎変調 ~ひずみ波の使われ方とAM変調度の求め方
◎復調 ~ひずみ波から特定の周波数を取り出す方法
