今回は、「交流電圧の実効値の求め方(正弦波編)」についての説明です。
周期T[s]の交流電圧v(t)の実効値Vrmsは、以下のように定義されています。
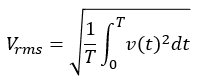
交流電圧の実効値の定義式
周期T[s]の交流電圧v(t)の実効値Vrmsは、以下のように定義されています。
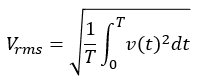
この定義式は、交流電圧を2乗して0~Tの範囲(1周期)で積分して周期Tで割ったものを平方根にしています。
つまり、2乗(Square)し、平均(Mean)し、平方根(Root)にした値になっているわけです。
このことを略してRMS(※実効値のこと)と呼ぶので、単純にその関係を式に当て嵌めたものが定義式になっているということです。
ただ、これでは何故2乗(Square)し、平均(Mean)し、平方根(Root)にすると実効値になるのかわからないですよね?
ということで、まずは定義式を用いないで別口から実効値を求めてみます。
定義式を用いない正弦波交流の実効値の求め方
抵抗に交流電圧を与えた際の電力と、同じ抵抗に直流電圧を与えた際の電力が等しくなる時、この交流電圧(電流)の実効値は直流電圧(電流)と等しくなると定義されています。
これを踏まえて実効値を求めていきます。
まず、図1のような抵抗R[Ω]に直流電源VDCを繋いだ単純な回路があるとします。
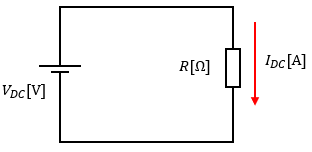
この時、抵抗Rの電力は、PDC=VDCIDCです。
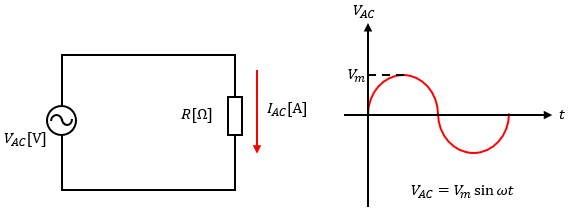
なので、図2のように直流電源VDCを交流電源VAC=Vmsinωtに入れ替えた時の抵抗Rの電力PACを計算し、PDC=PACになるためのVmを求めることで実効値を算出します。
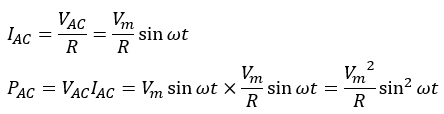
「2倍角の公式」を用いてsinの2乗を変形します。
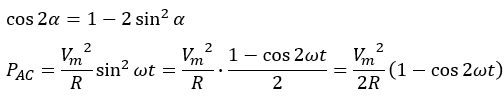
このPACを図示すると、図3のようになります。
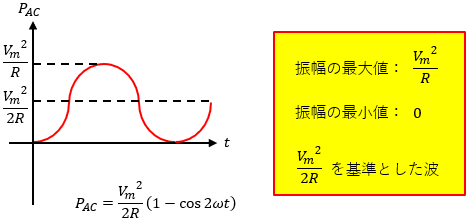
Vm2/2Rを基準とした波になることがわかるので、PACの平均値はVm2/2Rになるとわかります。
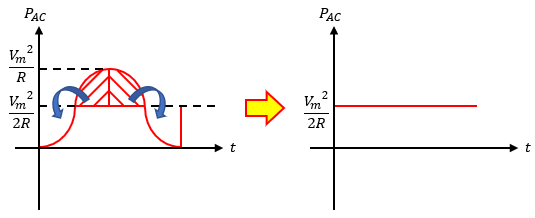
このPACの平均値がPDCと等しくなる時の交流電圧(電流)が実効値になるわけです。
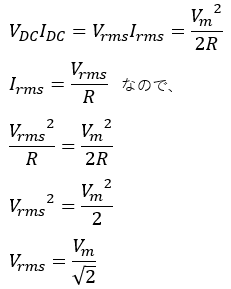
これで正弦波交流の実効値はVm/√2になると求めることができました。
だから交流の実効値は2乗(Square)し、平均(Mean)し、平方根(Root)にした値と呼ばれているわけです。
定義式を用いた正弦波交流の実効値の求め方
次は、定義式を使って正弦波の実効値を実際に求めてみます。
v(t)は先程のVAC同様にVmsinωtだとします。
この式を定義式に代入し、計算していきます。
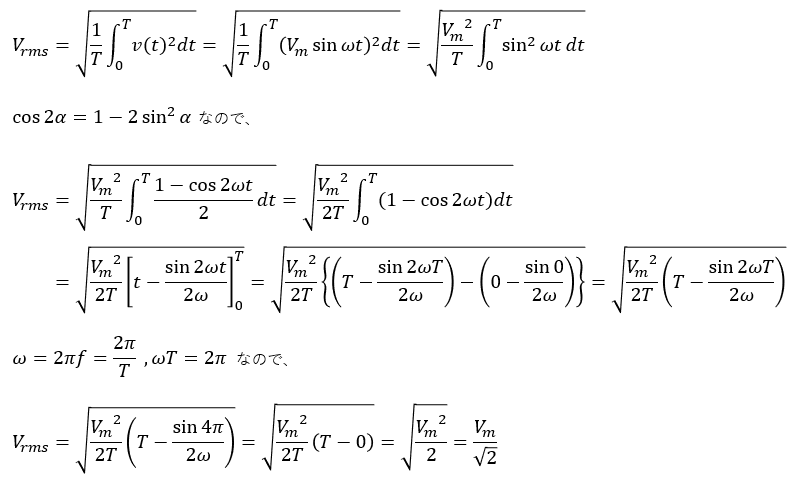
「正弦波交流の平均値と実効値」で述べた実効値は、実際はこのように求めているのです。
以上、「交流電圧の実効値の求め方(正弦波編)」についての説明でした。
【基礎から学ぶ交流回路】
◎直流と交流の違い ~極性が変わらなければ交流ではない
◎正弦波交流 ~正弦波の周期と周波数
◎正弦波交流の位相のズレ
◎正弦波交流の平均値と実効値
◎交流電圧の平均値の求め方 ~正弦波編
◎交流電圧の実効値の求め方 ~正弦波編
◎交流電圧の平均値の求め方 ~三角波編
◎交流電圧の実効値の求め方 ~三角波編
◎整流形計器の平均値と実効値
◎正弦波交流のベクトル表示・フェザー表示
◎交流回路のオームの法則
◎交流電流の位相の変化 ~リアクタンス成分は位相がπ/2ズレる
◎R-L-C直列回路のポイント ~インピーダンスの三角形を描け!
◎R-L-C並列回路のポイント ~電流の三角形を描け!
◎交流回路の共振 ~直列共振と並列共振について
◎R-L-C直並列回路の共振
◎交流回路の電力 ~位相差による力率という考え方
◎交流回路のインピーダンスと電力の関係
◎交流回路のインピーダンスの複素数表示
◎交流回路の電力の複素数表示
◎交流ブリッジ回路と平衡条件
◎過渡現象と時定数
◎R-L-C直並列回路の定常状態の考え方
◎ひずみ波 ~基本波・高調波とは?
◎ひずみ波の消費電力 ~抵抗で消費される平均電力の求め方
◎変調 ~ひずみ波の使われ方とAM変調度の求め方
◎復調 ~ひずみ波から特定の周波数を取り出す方法
