今回は、「交流回路の電力の複素数表示」についての説明です。
皮相電力S、有効電力P、無効電力Qは複素数表示すると以下のようになります。
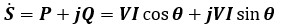
複素電力Sは複素電圧Vの共役複素数と複素電流Iの積となる。
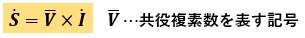
交流回路の電力の複素数表示
『そもそも複素数って何?』という方はこちら(工事中)へどうぞ。
「交流回路の電力」にて、皮相電力S、有効電力P、無効電力Qで電力の直角三角形を作ることができると述べました。
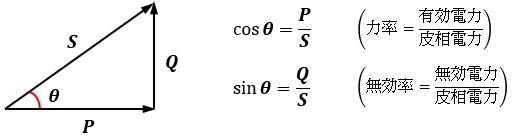
この電力の関係を複素数で表すと以下のようになります。
※ 電圧Vを基準にして、電流Iがθ進んでいる場合について考えています。
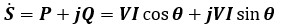
この電力のことを複素電力と呼びます。
(複素数表示したものは総じて「複素~」と呼びます)
ちなみに、無効電力Qが虚数扱いになっています。
虚数を表す「j」が分子にあると位相がπ/2進んでいる、分母にあると位相がπ/2遅れていることを意味しています。
複素電力の計算
複素電力Sは、複素電圧Vと複素電流Iの積で求めることも可能です。
ベクトル表示でV=V∠α[V]、I=I∠β[A]の電圧と電流があります。
複素電圧Vと複素電流Iの位相差θはθ=α-βです。
位相差を明確にする為に、横軸に複素電圧Vを合わせて基準にします。
その為、両ベクトルをαだけ時計回りに回転させます。
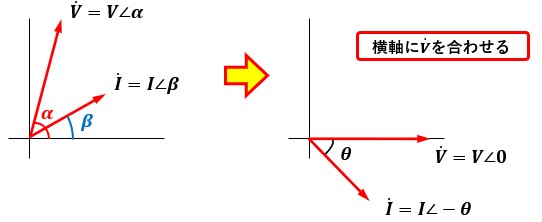
ここで、(回転後の複素電圧V)×(回転後の複素電流I)=(回転前の複素電圧の共役複素数)×(回転前の複素電流I)という関係が成り立っている為、複素電力Sは以下のように表せます。
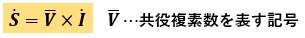
計算の結果、虚数部の符号が+の時は進み、-の時は遅れの無効電力になります。
ちなみに、横軸に複素電流Iを合わせても計算はできますが、進み・遅れの見方が複素電圧Vを基準にした時と反対にする必要があります。
ややこしいので基本は電圧を基準にしましょう。
『(回転後の複素電圧V)×(回転後の複素電流I)=(回転前の複素電圧の共役複素数)×(回転前の複素電流I)という関係が何故成り立っているのか?』、『共役複素数って何だっけ?』という方は以下の説明をご覧下さい。
実例を用いた説明を記載してあります。
以下のような複素電圧Vと複素電流Iがあります。
この時の複素電力Sを求めてみましょう。
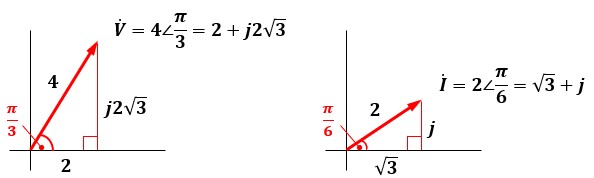
電圧を基準にしたいので、各々π/3だけ時計回りに回転させます。
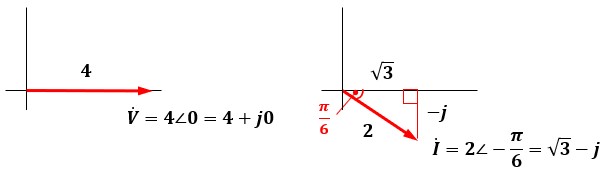
ベクトル表示のまま計算し、複素電力Sを求めると以下のようになります。
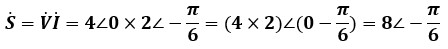
ベクトルの掛け算は、大きさ同士、角度同士で別々に計算します。
ここで、回転させる前後の複素電圧Vと複素電流Iに注目して下さい。
ベクトル表示の場合、π/3時計回りに回転させても変化するのは角度だけですよね?
つまり、複素電圧Vと複素電流Iを各々π/3ずつ回転させて掛け合わせたベクトルと、複素電圧Vを2π/3回転させて複素電流Iと掛け合わせたベクトルは一致します。
試しに、後者で計算してみましょう。
複素電圧Vを2π/3だけ時計回りに回転させて、複素電力Sを求めます。
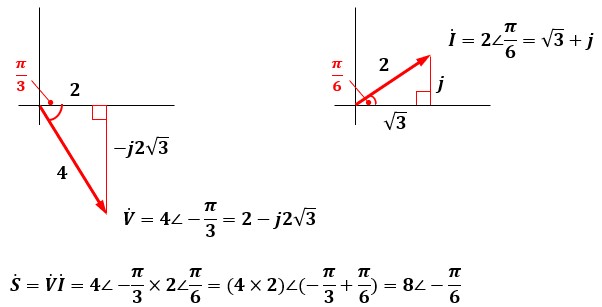
計算の結果、複素電力Sの値が一致することがわかりました。
では、複素電圧Vを2π/3だけ時計回りに回転させるということは何を意味しているでしょうか?
図を見比べてわかる通り、横軸に対して元のベクトルを反転させている、線対称にしています。
この、軸に対して反転・線対称になる複素数のことを共役複素数と呼びます。
つまり、複素電力Sは複素電圧Vの共役複素数と複素電流Iの積となります。
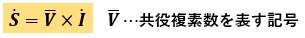
ちなみに、共役複素数は複素数表示の時は虚数部の符号を反転させた値、ベクトル表示の時は角度の符号を反転させた値となります。
以上、「交流回路の電力の複素数表示」についての説明でした。
【基礎から学ぶ交流回路】
◎直流と交流の違い ~極性が変わらなければ交流ではない
◎正弦波交流 ~正弦波の周期と周波数
◎正弦波交流の位相のズレ
◎正弦波交流の平均値と実効値
◎交流電圧の平均値の求め方 ~正弦波編
◎交流電圧の実効値の求め方 ~正弦波編
◎交流電圧の平均値の求め方 ~三角波編
◎交流電圧の実効値の求め方 ~三角波編
◎整流形計器の平均値と実効値
◎正弦波交流のベクトル表示・フェザー表示
◎交流回路のオームの法則
◎交流電流の位相の変化 ~リアクタンス成分は位相がπ/2ズレる
◎R-L-C直列回路のポイント ~インピーダンスの三角形を描け!
◎R-L-C並列回路のポイント ~電流の三角形を描け!
◎交流回路の共振 ~直列共振と並列共振について
◎R-L-C直並列回路の共振
◎交流回路の電力 ~位相差による力率という考え方
◎交流回路のインピーダンスと電力の関係
◎交流回路のインピーダンスの複素数表示
◎交流回路の電力の複素数表示
◎交流ブリッジ回路と平衡条件
◎過渡現象と時定数
◎R-L-C直並列回路の定常状態の考え方
◎ひずみ波 ~基本波・高調波とは?
◎ひずみ波の消費電力 ~抵抗で消費される平均電力の求め方
◎変調 ~ひずみ波の使われ方とAM変調度の求め方
◎復調 ~ひずみ波から特定の周波数を取り出す方法
