今回は、「CMOS論理回路」についての説明です。
p型MOSFETとn型MOSFETの2種類のFETを組み合わせて構成した論理回路。
CMOS論理回路とは?
CMOS論理回路とは、p型MOSFETとn型MOSFETの2種類のFETを組み合わせて構成した論理回路のことです。
相補型(Complementary)MOS論理回路のことで、シーモス論理回路と読みます。
市場に出回っている論理演算素子の中身は大体このCMOS論理回路で構成されているようです。
論理回路における基本的な演算回路は以下のような種類がありました。
この内、NOT回路・NAND回路・NOR回路をCMOS論理回路で表していきます。
おさらいとして、MOSFETの図記号は以下のようになっています。
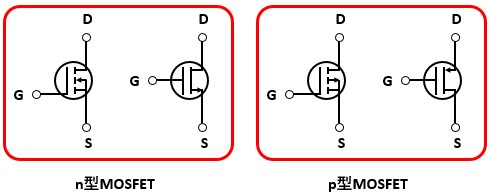
MOSFETって微妙に色んなパターンで描かれていることがあるんですよね。
FETはゲートに電圧を印加した際の電界によってキャリアの動きを制御します。
n型MOSFETは、ゲートに電圧を印加した時にドレイン-ソース間に電流が流れるようになります。
p型MOSFETは、ゲートに電圧を印加していない時にドレイン-ソース間に電流が流れるようになります。
FETについてもう少し詳しく知っておきたい場合ば以下の記事をご覧ください。
CMOS論理回路(NOT回路)
NOT回路をCMOS論理回路で表すと以下のようになります。
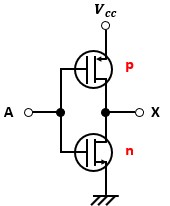
本当にNOT回路になっているのか確認してみましょう。
電圧が印加されている時を”1″、電圧を印加していない時(GND接続)を”0″と考えます。
端子Aに電圧を印加した時は、n型MOSFETがON・p型MOSFETがOFFになるので、端子XはGNDに繋がります。
端子Aに電圧を印加していない時は、n型MOSFETがOFF・p型MOSFETがONになるので、端子XはVccに繋がります。
つまり、端子Aが”0″の時は端子Xは”1″、端子Aが”1″の時は端子Xは”0″という関係が成り立っています。
よって、図2はNOT回路だと言えます。
CMOS論理回路(NAND回路)
NAND回路をCMOS論理回路で表すと以下のようになります。
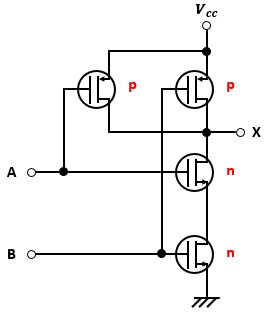
見た目が一気にややこしくなりましたが、実は構造は単純です。
というのも、よくよく見るとNOT回路を2つ直列接続しているだけなんですよね。
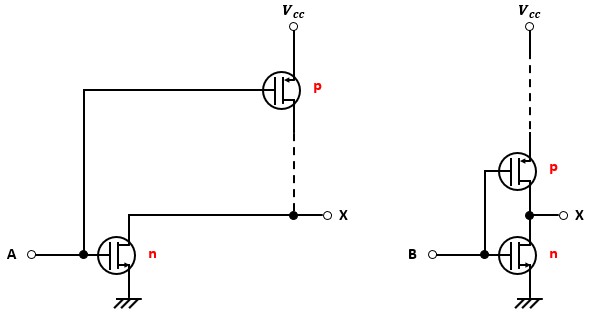
端子Aに関係する回路、端子Bに関係する回路に分けて見ると以下のようになります。
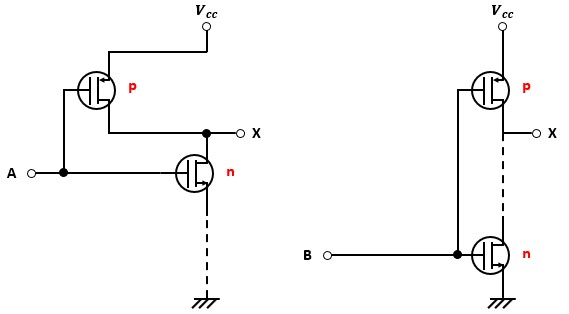
それぞれNOT回路になっているでしょう?
この2つの回路を同時に満たしてる回路がNAND回路なので、出力を一纏めにして端子Xに集結させた結果、図3のような回路になっているわけです。
CMOS論理回路(NOR回路)
NOR回路をCMOS論理回路で表すと以下のようになります。
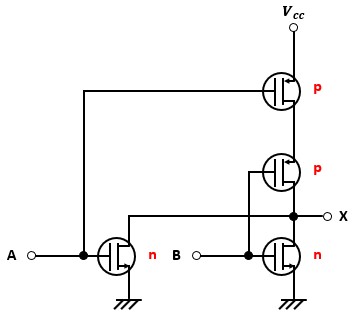
NAND回路の説明で察しているのではないかと思いますが、NOR回路はNOT回路を並列接続しているだけです。
以上、「CMOS論理回路」についての説明でした。
【基礎から学ぶ論理回路】
◎アナログとデジタルの違い ~論理回路を学ぶ前提知識
◎論理的演算とはそもそも何なのか
◎真偽と真理値表
◎交換則と分配則
◎ド・モルガンの定理
◎カルノー図を用いた論理式の表し方
◎カルノー図を用いた論理式の簡単化
◎論理ゲートのAND・OR・NOT回路
◎論理ゲートのNAND・NOR・XOR回路
◎論理回路の考え方 ~実際の回路と論理式の関係
◎組み合わせ論理回路の考え方 ~論理式を論理ゲートで表す
◎ド・モルガンの等価ゲート
◎ド・モルガンの等価ゲートを用いた回路の簡単化
◎CMOS論理回路 ~論理ゲートを構成する実際の回路
◎CMOS論理回路の組み合わせ

