【基礎から学ぶ直流回路】基準点による電位の変化

基本的に”イメージ”を意識した内容となっておりますので、基礎知識の無い方への入門向きです。
じっくり学んでいきましょう！

今回は、「基準点による電位の変化」についての説明です。

基準点による電位の変化

あくまでGNDが0[V]になる。

図1のような回路があったとします。

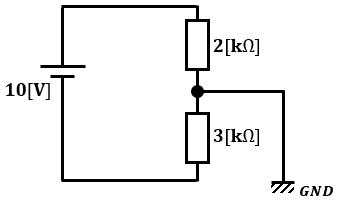
なんか変なところにGNDが繋がっていますよね。
この場合、2kΩ抵抗と3kΩ抵抗の両端の電位がどうなるかわかりますか？
おそらくよくわからなくなる人が多いのではないでしょうか？

この場合、注意するべき点はただ一点です。

あくまでGNDが0[V]です。
電源のマイナス側は0Vとは限らないのです。

では、実際にどうなるのか解説していきますね。

まず、GNDが変なところに繋がっていない場合の2kΩ抵抗と3kΩ抵抗の両端の電位差(各抵抗での電圧降下)を求めましょう。

オームの法則から、回路全体に流れる電流は10[V]÷5[kΩ]=2[mA]です。
なので、2kΩ抵抗は2[kΩ]×2[mA]=4[V]、3kΩ抵抗は3[kΩ]×2[mA]=6[V]。
これが2kΩ抵抗と3kΩ抵抗の両端の電位差です。

このタイミングでGND(基準点：0[V])について考えます。

あくまでこのGNDが0[V]です。
なので、2kΩと3kΩの中間地点は0[V]になります。

2kΩ抵抗と3kΩ抵抗の中間が0[V]で、2kΩ抵抗の両端の電位差が4[V]、3kΩ抵抗の両端の電位差が6[V]です。
その為、この回路の電位の関係を整理すると図2のようになります。

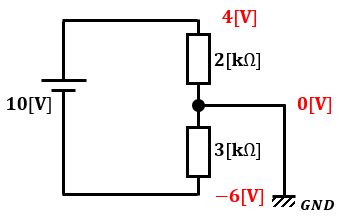
見慣れていないと違和感がすごいと思いますが、考え方はこれで合ってます。
どこが0[V]なのかしっかり考えましょうね。

以上、「基準点による電位の変化」についての説明でした。

【基礎から学ぶ直流回路】

NewsTag