【基礎から学ぶ交流回路】 交流回路の共振 ～直列共振と並列共振について

今回は、「交流回路の共振」についての説明です。

交流回路には、共振と呼ばれる状態があります。
R－L－C直列回路とR－L－C並列回路で異なる共振の仕方をする為、それぞれ説明していきます。

R－L－C直列回路の共振

まずは、R－L－C直列回路の共振について説明します。
通常、R－L－C直列回路の「インピーダンスの三角形」は図1のようになっています。

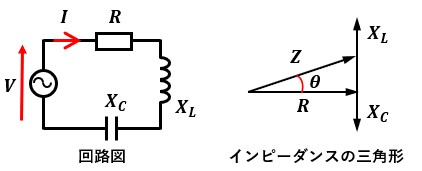
図1では、X_L＞X_Cなので上側のベクトル分の方が大きく、このような三角形を描いています。
つまり、誘導性リアクタンスX_L＝容量性リアクタンスX_Cの場合、X_LとX_Cが互いに打ち消し合うことでベクトル和が0になることがわかります。

直列回路では電流Iは一定なので、X_L＝X_Cの時にX_LI＝X_CIが成り立ちます。
V_L=X_LI、V_C=X_CIなので、X_Lにかかる電圧V_LとX_Cにかかる電圧V_Cのベクトル和が0になることがわかります。

この状態のことを直列共振と呼びます。

R－L－C並列回路の共振

次に、R－L－C並列回路の共振について説明します。
通常、R－L－C並列回路の「電流の三角形」は図2のようになっています。

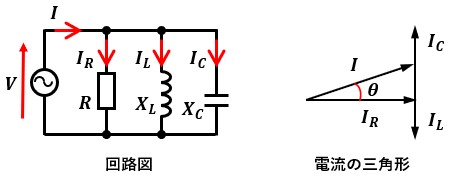
図2では、I_C＞I_Lなので上側のベクトル分の方が大きく、このような三角形を描いています。
つまり、誘導性リアクタンスX_Lに流れる電流I_L＝容量性リアクタンスX_Cに流れる電流I_Cの場合、I_LとI_Cが互いに打ち消し合うことでベクトル和が0になることがわかります。

では、I_LとI_Cの大きさが等しくなる条件は何でしょう？
並列回路では電圧Vは一定なので、X_LI_L＝X_CI_Cが成り立ちます。
ここでX_L＝X_Cだとすると、X_LI_L＝X_LI_Cとなり、I_L=I_Cとなります。
つまり、X_L＝X_Cの時にX_Lに流れる電流I_LとX_Cに流れる電流I_Cのベクトル和が0になると言えます。

この状態のことを並列共振と呼びます。

共振の条件

以上より、交流回路の共振条件は直列共振・並列共振問わずにX_L＝X_Cとなります。

ここで、共振時の周波数をf₀、角速度をω₀とすると、以下の関係が成り立ちます。

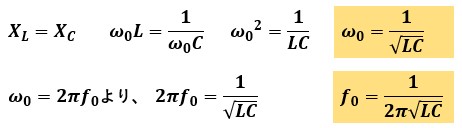
以上、「交流回路の共振」についての説明でした。

---

【基礎から学ぶ交流回路】

◎直流と交流の違い ～極性が変わらなければ交流ではない
◎正弦波交流 ～正弦波の周期と周波数
◎正弦波交流の位相のズレ
◎正弦波交流の平均値と実効値
◎交流電圧の平均値の求め方 ～正弦波編
◎交流電圧の実効値の求め方 ～正弦波編
◎交流電圧の平均値の求め方 ～三角波編
◎交流電圧の実効値の求め方 ～三角波編
◎整流形計器の平均値と実効値
◎正弦波交流のベクトル表示・フェザー表示
◎交流回路のオームの法則
◎交流電流の位相の変化 ～リアクタンス成分は位相がπ/2ズレる
◎R－L－C直列回路のポイント ～インピーダンスの三角形を描け！
◎R－L－C並列回路のポイント ～電流の三角形を描け！
◎交流回路の共振 ～直列共振と並列共振について
◎R－L－C直並列回路の共振
◎交流回路の電力 ～位相差による力率という考え方
◎交流回路のインピーダンスと電力の関係
◎交流回路のインピーダンスの複素数表示
◎交流回路の電力の複素数表示
◎交流ブリッジ回路と平衡条件
◎過渡現象と時定数
◎R－L－C直並列回路の定常状態の考え方
◎ひずみ波 ～基本波・高調波とは？
◎ひずみ波の消費電力 ～抵抗で消費される平均電力の求め方
◎変調 ～ひずみ波の使われ方とAM変調度の求め方
◎復調 ～ひずみ波から特定の周波数を取り出す方法