今回は、「交流回路の電力」についての説明です。
交流回路の電力
交流回路は直流回路と違い、電圧と電流に位相差があります。
その関係上、交流回路の電力は皮相電力S、有効電力P、無効電力Qについて考慮する必要があります。
では、それぞれの電力が何を示しているのか解説していきます。
直流回路の場合、常に電流と電圧のベクトルは同じ方向を向いていました。
この時の電力PはP=VIと表すことができました。
この電流と電圧のベクトルが合っている状態での電力が実際に消費される電力となります。
交流回路の場合、電圧と電流に位相差がある為、ベクトルの向きが一致していません。
図1のように電圧と電流に位相差θがあるとします。
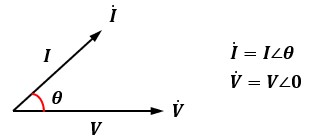
位相差を考慮せずに、電流と電圧の大きさをかけた値を皮相電力と呼びます。
量記号はS、単位は[VA]です。
式で表すと、S=VIとなります。
皮相電力は実際に消費される電力ではなく、あくまで見かけ上の電力です。
電流と電圧の位相差を考慮していない為、実際の消費電力よりも大きい値となっています。
位相差を考慮してベクトルの向きを合わせた時の消費電力を有効電力と呼びます。
量記号はP、単位は[W]です。
式で表すと、P=VIcosθとなります。
有効電力は負荷で実際に消費される電力です。
ここで出てきたcosθは力率といい、有効になる割合を表しています。
VIcosθを有効電力と呼ぶのに対し、VIsinθを無効電力と呼びます。
量記号はQ、単位は[var]です。
無効電力は、仕事をせずに電源に回帰する電力とのことです。
今は深く考えないようにしましょう。
ここで出てきたsinθは無効率といいます。
ここまで説明した皮相電力S、有効電力P、無効電力Qは、電力の直角三角形として表すことが可能です。
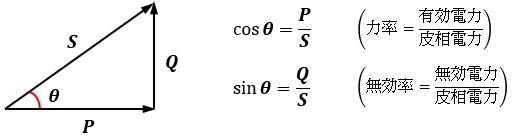
以上の関係からわかる通り、力率cosθは有効電力Pと皮相電力Sの比、無効率sinθは無効電力Qと皮相電力Sの比となります。
以上、「交流回路の電力」についての説明でした。
【基礎から学ぶ交流回路】
◎直流と交流の違い ~極性が変わらなければ交流ではない
◎正弦波交流 ~正弦波の周期と周波数
◎正弦波交流の位相のズレ
◎正弦波交流の平均値と実効値
◎交流電圧の平均値の求め方 ~正弦波編
◎交流電圧の実効値の求め方 ~正弦波編
◎交流電圧の平均値の求め方 ~三角波編
◎交流電圧の実効値の求め方 ~三角波編
◎整流形計器の平均値と実効値
◎正弦波交流のベクトル表示・フェザー表示
◎交流回路のオームの法則
◎交流電流の位相の変化 ~リアクタンス成分は位相がπ/2ズレる
◎R-L-C直列回路のポイント ~インピーダンスの三角形を描け!
◎R-L-C並列回路のポイント ~電流の三角形を描け!
◎交流回路の共振 ~直列共振と並列共振について
◎R-L-C直並列回路の共振
◎交流回路の電力 ~位相差による力率という考え方
◎交流回路のインピーダンスと電力の関係
◎交流回路のインピーダンスの複素数表示
◎交流回路の電力の複素数表示
◎交流ブリッジ回路と平衡条件
◎過渡現象と時定数
◎R-L-C直並列回路の定常状態の考え方
◎ひずみ波 ~基本波・高調波とは?
◎ひずみ波の消費電力 ~抵抗で消費される平均電力の求め方
◎変調 ~ひずみ波の使われ方とAM変調度の求め方
◎復調 ~ひずみ波から特定の周波数を取り出す方法
