今回は、「電圧源と電流源を含む回路の考え方」についての説明です。
電圧源は短絡、電流源は開放して考える。
電圧源と電流源の両方を含む回路
電圧源もしくは電流源にいくつかの抵抗を繋いだだけの回路ならばオームの法則なりキルヒホッフの法則なりを用いれば各抵抗の端子電圧や電流を計算することは容易です。
ですが、図1のように電圧源と電流源が両方存在する場合はどうでしょう?
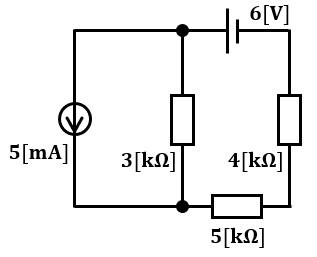
どこかしらで演習問題を解いたことがある方は迷うことはないかもしれませんが、電圧源と電流源という存在を教科書で知った程度の知識量の場合はイマイチどうすれば良いのかわからないのではないでしょうか?
私も最初は普通にわからなかったです。
ということで、今回は電圧源と電流源の両方を含む回路にて抵抗の端子電圧や電流を求める方法について説明していこうと思います。
電圧源と電流源の両方を含む回路の考え方
考え方についてですが、基本は重ね合わせの理を使えば解けます。
重ね合わせの理を使用する際に、電圧源は短絡、電流源は開放して考えるのがポイントです。
これは、理想的な電圧源は内部抵抗が0Ω、理想的な電流源は内部抵抗が無限大であることが起因しています。
内部抵抗が0Ωということは電流の流れを阻害しないので短絡に値し、抵抗が無限大だということは電流は一切流れなくなるので開放と同義だということです。
重ね合わせの理を用いる際、電圧源が複数あった場合は図2のように電源が単独に存在する回路として考えました。
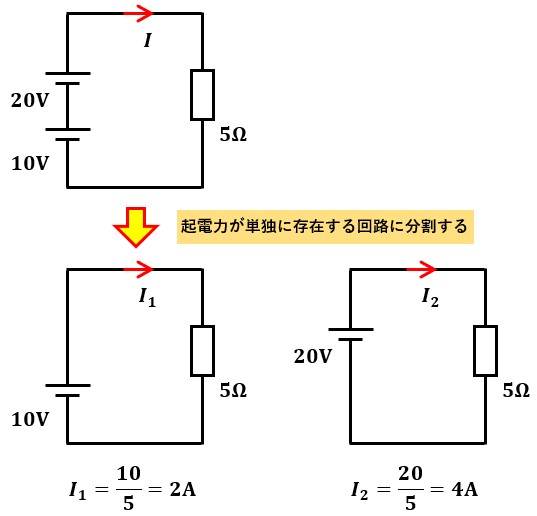
これは、厳密には1つの電圧源を除く電圧源を全て短絡した状態にして考えていたわけです。
言葉で説明してもわかりづらいので、例に沿って考えてみましょう。
図1に示した回路にて、4kΩ抵抗に流れる電流を求めます。
まずは、電圧源が4kΩ抵抗に流す電流について考えます。
先程述べた通り、電流源は開放して考えます。
つまり、図3のような回路になります。
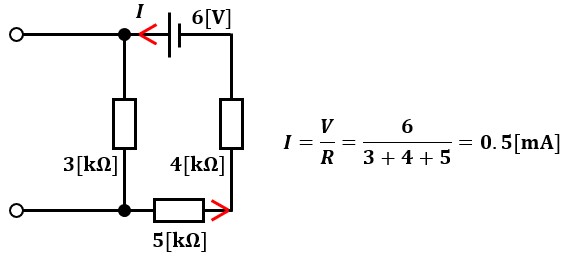
こうすると6Vの電圧源に3kΩ・4kΩ・5kΩの抵抗が直列に繋がれた単純な回路になる為、オームの法則から4kΩ抵抗に流れる電流は0.5mAだとわかります。
次は、電流源が4kΩ抵抗に流す電流について考えます。
電圧源は短絡して考えるので、図4のような回路になります。
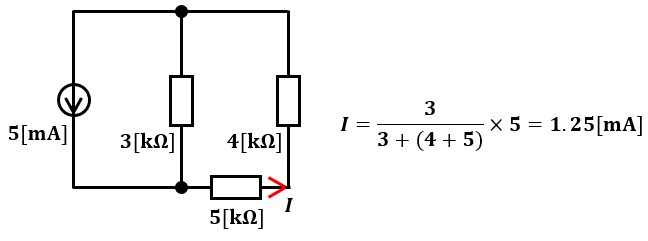
図4は電流源5mAに3kΩと9kΩ(4kΩと5kΩが直列)の抵抗を並列で接続した形となる為、分流させて値を求めます。
分流の考え方が苦手な方は、一度合成抵抗にかかる電圧を求めてから9kΩに流れる電流を求めましょう。
電圧源と電流源から4kΩ抵抗に供給される電流の向きは同じなので、4kΩ抵抗に流れる電流は0.5mA+1.25mA=1.75mAとなります。
電圧源と電流源が両方含まれている回路であっても、こんな具合に重ね合わせの理を用いて計算していくことが可能です。
以上、「電圧源と電流源を含む回路の考え方」についての説明でした。
【基礎から学ぶ直流回路】
◎電気回路の基礎 ~そもそも電気回路とは?
◎同じ[V]という単位に対して量記号が”E”と”V”に分かれている理由
◎回路図の描き方 ~初心者は知っておきたい基本的なルール
◎抵抗の基礎 ~種類やカラーコードの見方
◎直列接続の考え方
◎並列接続の考え方
◎抵抗と並列に導線を繋いだ場合の電流の流れ
◎基準点による電位の変化
◎導体の電気抵抗 ~抵抗率と導電率の関係
◎キルヒホッフの法則
◎重ね合わせの理
◎テブナンの定理
◎ノートンの定理
◎テブナンの定理とノートンの定理の関係
◎ミルマンの定理
◎ブリッジ回路と平衡条件
◎ホイートストンブリッジ回路とメートルブリッジ回路
◎ブリッジ回路のΔ-Y変換
◎電圧源と電流源 ~等価電源と理想電源の違い
◎電圧源と電流源を含む回路の考え方
◎電圧源と電流源の接続方法の注意点
◎起電力と内部抵抗が等しい電圧源を複数並列に繋いだ場合の考え方
◎電力とジュールの法則
◎チップ抵抗器の定格電力と外形寸法表記
◎最大電力 ~最小定理の考え方
◎複数の電源から供給される電力の割合
