【基礎から学ぶ交流回路】 R－L－C並列回路のポイント ～電流の三角形を描け！

今回は、「R－L－C並列回路のポイント」についての説明です。

抵抗R、誘導性リアクタンスX_L、容量性リアクタンスX_Cが並列接続されている場合、この3要素の各々に流れる電流で直角三角形を作ると斜辺が合成電流になります。
実際にどう考えるのか、R－L並列回路、R－C並列回路、R－L－C並列回路の3パターンを用いて説明していきます。

R－L並列回路

抵抗Rと誘導性リアクタンスX_Lを並列接続した場合、図1のような電流の直角三角形が描けます。

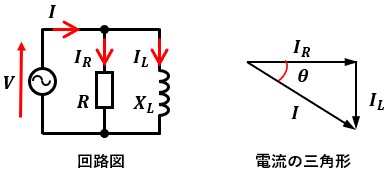
抵抗Rに流れる電流I_Rを基準とした時、誘導性リアクタンスX_Lに流れる電流I_Lは下向きに描きます。

合成電流Iの大きさと、IとI_Rのなす角θは以下のように表せます。

電流Iは電圧Vより角度θだけ位相が遅れます。

R－C並列回路

抵抗Rと容量性リアクタンスX_Cを並列接続した場合、図2のような電流の直角三角形が描けます。

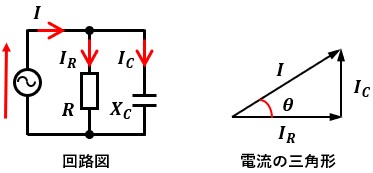
抵抗Rに流れる電流I_Rを基準とした時、容量性リアクタンスX_Cに流れる電流I_Cは上向きに描きます。

合成電流Iの大きさと、IとI_Rのなす角θは以下のように表せます。

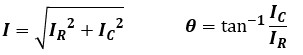
電流Iは電圧Vより角度θだけ位相が進みます。

R－L－C並列回路

抵抗R、誘導性リアクタンスX_L、容量性リアクタンスX_Cを並列接続した場合、図3のような電流の直角三角形が描けます。
※ I_L＜I_Cの場合を例としています。

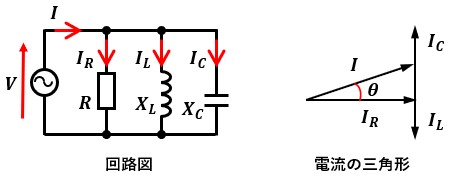
抵抗Rに流れる電流I_Rを基準とした時、誘導性リアクタンスX_Lに流れる電流I_Lは下向き、容量性リアクタンスX_Cに流れる電流I_Cは上向きに描き、両方の成分が存在する場合は互いに打ち消し合います。

合成電流Iの大きさと、IとI_Rのなす角θは以下のように表せます。

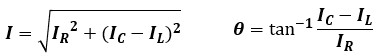
I_L＞I_Cの時は電流Iは電圧Vより角度θだけ位相が遅れ、I_L＜I_Cの時は電流Iは電圧Vより角度θだけ位相が進みます。

以上、「R－L－C並列回路のポイント」についての説明でした。

---

【基礎から学ぶ交流回路】

◎直流と交流の違い ～極性が変わらなければ交流ではない
◎正弦波交流 ～正弦波の周期と周波数
◎正弦波交流の位相のズレ
◎正弦波交流の平均値と実効値
◎交流電圧の平均値の求め方 ～正弦波編
◎交流電圧の実効値の求め方 ～正弦波編
◎交流電圧の平均値の求め方 ～三角波編
◎交流電圧の実効値の求め方 ～三角波編
◎整流形計器の平均値と実効値
◎正弦波交流のベクトル表示・フェザー表示
◎交流回路のオームの法則
◎交流電流の位相の変化 ～リアクタンス成分は位相がπ/2ズレる
◎R－L－C直列回路のポイント ～インピーダンスの三角形を描け！
◎R－L－C並列回路のポイント ～電流の三角形を描け！
◎交流回路の共振 ～直列共振と並列共振について
◎R－L－C直並列回路の共振
◎交流回路の電力 ～位相差による力率という考え方
◎交流回路のインピーダンスと電力の関係
◎交流回路のインピーダンスの複素数表示
◎交流回路の電力の複素数表示
◎交流ブリッジ回路と平衡条件
◎過渡現象と時定数
◎R－L－C直並列回路の定常状態の考え方
◎ひずみ波 ～基本波・高調波とは？
◎ひずみ波の消費電力 ～抵抗で消費される平均電力の求め方
◎変調 ～ひずみ波の使われ方とAM変調度の求め方
◎復調 ～ひずみ波から特定の周波数を取り出す方法