今回は、「正弦波交流」についての説明です。
正弦波交流
正弦波交流とは、電圧や電流が正弦波状に変化するもののことです。
ちなみに、交流は時間経過で周期的に大きさ及び正負の符号が変化する電流のことです。
『正弦波状』という言葉に不安を覚える方は以下の記事も参考にしてみてください。
交流電源を負荷に繋いだ単純な回路と、交流電源の波形を図1に示します。
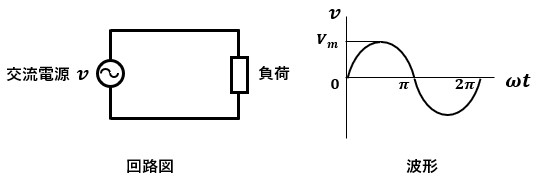
交流電源は、円の中に正弦波が描かれた図記号になります。
波形は、横軸を時間tと角度ωtの2パターンで表す場合があります。
この正弦波交流電圧vを式で表すと以下のようになります。
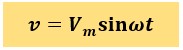
vは瞬時値です。単位は[V]。正弦波交流は時間tの経過により常に変化する為、その時々の値(瞬時値)を示しています。
Vmは最大値(maximum)です。単位は[V]。正弦波交流のピーク値を示しています。
sinは正弦波です。サインカーブとも呼びます。
ωは角速度です。単位は[rad/s]。1秒間にどの程度の速度で角度が変化するかを表しています。
tは時間です。単位は[s]。
角速度ωの補足説明です。
radは角度を表す手法で、弧度とも呼びます。
2π[rad]は360°なので、角速度ω=2π[rad/s]の時には1秒間に360°角度が変化します。
その為、横軸ωtの正弦波交流は、角度が2π変化すると1周して元の位置に戻ってきます。
角速度ωは以下のように表すことができます。
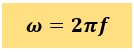
fは周波数です。単位は[Hz]。
周波数は、1秒間に何回波が変化するかという回数を示しています。
ωは単位の[rad/s]からもわかる通り1秒毎の角度の変化を表していました。
正弦波交流の1回の変化は2π[rad]に当たる為、角度は1秒間に2π[rad]×f[回]分変化するということになります。
この関係からω=2πfという式が導き出されています。
関係がわかりづらいと思う方は図でイメージしましょう。
図2のように1秒間に6π角度が変化する正弦波交流があるとします。
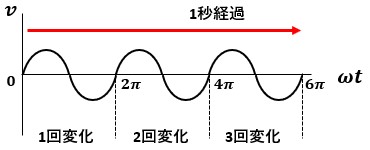
- 1秒間に6π角度が変化しているので、角速度ω=6π[rad/s]です。
- 1秒間に変化している回数が3回なので、周波数f=3[Hz]です。
- 1回の変化で角度は2π変化します。
1秒間に6π角度が変化している(ω)=2πの角度の変化を1秒間に3回繰り返している(2πf)
なので、ω=2πfが成り立っています。
ちなみに、周波数fの逆数は周期Tです。
式で表すと、f=1/Tとなります。
周期の単位は[s]です。
周波数は1秒間に何回変化するかを表していたので、逆数である周期は1回変化するのにどの程度時間を要するかを表しています。
先程の1秒間に3回変化していた正弦波交流の図を見ながら考えるとしっくりくるかと思います。
比で考えると、「1秒間:3回変化=?秒間:1回変化」と表せます。
ここで言う「3回変化」は周波数f=3[Hz]であることを指している為、「3回変化」の部分は「周波数f」に置き換えることができます。
⇒「1秒間:f=?秒間:1回変化」
また、1回変化するのにかかる時間は周期Tなので、「?秒間」の部分は「周期T」に置き換えることができます。
⇒「1秒間:f=T:1回変化」
以上の関係から、T=1/fの関係を導き出せます。
また、f=3[Hz]を代入することで周期T=1/3[s]であることがわかります。
以上、「正弦波交流」についての説明でした。
【基礎から学ぶ交流回路】
◎正弦波交流 ~正弦波の周期と周波数
◎正弦波交流の位相のズレ
◎正弦波交流の平均値と実効値
◎正弦波交流のベクトル表示
◎交流回路のオームの法則
◎交流電流の位相の変化
◎R-L-C直列回路のポイント
◎R-L-C並列回路のポイント
◎交流回路の共振
◎交流回路の電力
◎交流回路のインピーダンスと電力の関係
◎交流回路のインピーダンスの複素数表示
◎交流回路の電力の複素数表示
◎交流ブリッジ回路と平衡条件
◎過渡現象と時定数
◎ひずみ波 ~基本波・高調波とは?
◎復調 ~ひずみ波から特定の周波数を取り出す方法

