【基礎から学ぶ論理回路】アナログとデジタルの違い～論理回路を学ぶ前提知識

基本的に”イメージ”を意識した内容となっておりますので、基礎知識の無い方への入門向きです。
じっくり学んでいきましょう！

今回は、「アナログとデジタルの違い」についての説明です。

・初めに
・アナログとデジタルの違い
・AD/DA変換
・デジタルデータの表し方

アナログとデジタルの違い

アナログは連続したデータ、デジタルは断続的なデータのこと。

初めに

論理回路って知っていますか？

論理回路は電気系の大学に進んでいるなら履修科目にあったのではないかと思いますが、一般的にはあまり知られていないかもしれないです。
ただ、電気や情報システム系の仕事に進むと、ICの動作やシーケンス制御などで論理演算回路が組まれていたりするので理解を余儀なくされます。

論理回路と言ったら基礎的なのはAND回路やOR回路やNOT回路などが挙げられるのですが、それの説明より前にそもそもアナログとデジタルの違いについて理解している必要があります。

今回は、まずはそちらの説明をしていこうと思います。

アナログとデジタルの違い

アナログとデジタルの違いを端的に述べると、以下のようになります。

アナログ

連続的なデータ

デジタル

断続的なデータ

言葉で表すと疑問符が浮かぶかもしれないので、実物の時計でイメージしてみましょう。

秒針・分針・時針が動く昔ながらの時計がありますよね。
アレがアナログ時計です。

アナログ時計の場合、常に針は動き続けています。
つまり、0時0分0秒と0時0分1秒の間にも秒針の動きが止まることはなく、その時々の”時間”というデータを常に指し示しているわけです。
だから連続したデータ=アナログです。

それに対してデジタル時計は、液晶画面に00:00:00という具合に時間表示されているものを指します。

時・分・秒を00:00:00という桁数で表示しているデジタル時計の場合、1秒(00:00:01)と2秒(00:00:02)は表示してくれますが、0.5秒は表示できませんよね？
このように、デジタル時計では1秒の次は2秒、2秒の次は3秒というように“時間”というデータの表示がぶつ切りになっているわけです。
だから断続的なデータ=デジタルです。

これがアナログとデジタルの違いですね。

AD/DA変換

基本的に自然現象のデータはアナログです。

仮に自然現象がデジタルだったとすると、温度が突然0℃から50℃に変化したり、車が突然0km/hから100km/hに加速する世界になります。
そんなこと起こり得るはずがないですよね。

その為、自然現象のデータをコンピュータに取り込む場合、最初はアナログデータの形になっています。
なのですが、アナログデータは値が流動的に変化するので、データとして管理するのに向いていません。
その時々で微小に値が変化しているので、細かすぎて再現性がないからです。
それに対してデジタルデータは、”0″か”1″かのように数値がはっきりしているので再現性が高いです。
ついでに言うと、値が変化しないのでノイズにも強いです。

なので、一般的にはアナログデータをデジタルデータに変換して取り込むことが多いです。
このことをアナログデータ(Analog)からデジタル(Digital)データに変換するのでAD変換と呼びます。
逆に、デジタル(Digital)データからアナログデータ(Analog)に変換することをDA変換と呼びます。

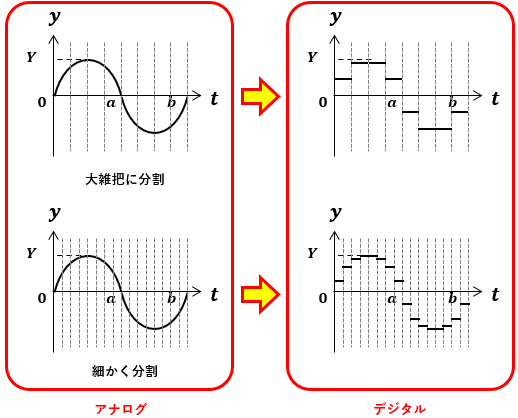
AD変換は、アナログデータを時間単位で細かくぶつ切り(サンプリング)にして平均値を求めた結果をデジタルデータとして表しているので、どうしても変換時に切り上げや切り捨てによる誤差が発生します。
なので、ぶつ切りにする間隔(サンプリング速度)を狭くしたり、デジタルデータでの表現桁数を増やすことで誤差を小さくすることが可能です。