今回は、「複数の電源から供給される電力の割合」についての説明です。
電源の接続方向により結果が変わる点に注意。
複数の電源から供給される電力の割合
電力P[W]には、P=VIという関係が成り立っています。
この関係を覚えていれば、1つの抵抗に1つの電源が接続された単純な回路における消費電力を求めるのは簡単です。
では、図1の電気回路を見てください。
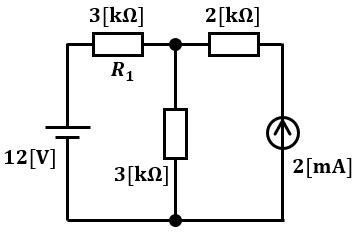
図1のように複数の電源、複数の抵抗が組み込まれた回路における抵抗R1の消費電力となるとどうでしょうか?
途端によくわからなくなりませんか?
ということで、今回は複数の電源が接続されている回路に供給される電力について考えていきます。
例として、図1のR1の電力について考えてみます。
P=VI=RI2の関係から、R1の消費電力はR1に流れる電流を求めれば計算することが可能です。
なので、各電源からR1に流れる電流を求める為に重ね合わせの理を使っていきます。
「電圧源と電流源を含む回路の考え方」で説明した通り、電圧源は短絡、電流源は開放して考えます。
まず、電圧源から流れる電流について考えてみましょう。
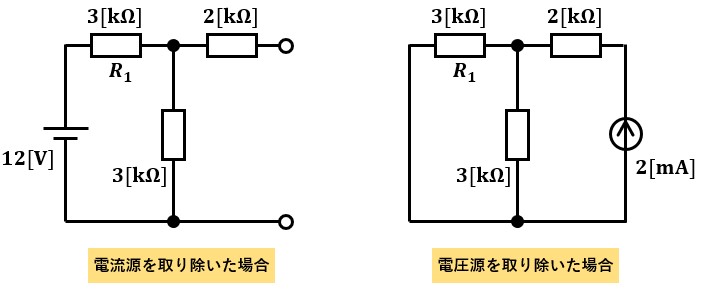
電流源を開放して考えるので、電圧源に関する回路は図2左のようになります。
すると、2[kΩ]抵抗には電圧がかからない為、12[V]の電源に6[kΩ]の抵抗が接続された単純な電気回路と見做せます。
なので、電圧源がR1に流す電流は2[mA]だとわかります。
次に、電流源から流れる電流について考えてみましょう。
電圧源を短絡して考えるので、電流源に関する回路は図2右のようになります。
2[kΩ]抵抗には電流源の2[mA]がそのまま流れ、並列回路では2[mA]が分流されます。
並列回路に関してはどちらの経路も抵抗値は同じ3[kΩ]になっているので、均等に1[mA]ずつに分かれます。
なので、電流源がR1に流す電流は1[mA]だとわかります。
以上より、R1に流れる電流は、電圧源から2[mA]、電流源から1[mA]だとわかりました。
つまり、合計で3[mA]の電流が流れる…と考えた方は間違いです。
電圧源と電流源からR1に流れる電流の向きを考えてみてください。
電圧源からは左から右、電流源からは右から左へ電流が流れますよね?
電流の向きが反対ということは、互いに打ち消し合うので足し算ではなく引き算になります。
結果、R1には電圧源から1[mA]の電流が供給されているということになります。
その為、R1の消費電力はP=(3×103)×(1×10-3)2=3[mW]となります。
このことから、R1に電力を供給している割合は電圧源が100%、電流源が0%という極端な結果になっていることがわかります。
仮に電流源が反対向きに繋がっていたとすると、R1に流れる電流が変化するので供給される電力の割合も変化します。
電源が複数繋がっていても接続の向きにより供給される電力の割合が変化するという点に注意しましょう。
以上、「複数の電源から供給される電力の割合」についての説明でした。
【基礎から学ぶ直流回路】
◎電気回路の基礎 ~そもそも電気回路とは?
◎同じ[V]という単位に対して量記号が”E”と”V”に分かれている理由
◎回路図の描き方 ~初心者は知っておきたい基本的なルール
◎抵抗の基礎 ~種類やカラーコードの見方
◎直列接続の考え方
◎並列接続の考え方
◎抵抗と並列に導線を繋いだ場合の電流の流れ
◎基準点による電位の変化
◎導体の電気抵抗 ~抵抗率と導電率の関係
◎キルヒホッフの法則
◎重ね合わせの理
◎テブナンの定理
◎ノートンの定理
◎テブナンの定理とノートンの定理の関係
◎ミルマンの定理
◎ブリッジ回路と平衡条件
◎ホイートストンブリッジ回路とメートルブリッジ回路
◎ブリッジ回路のΔ-Y変換
◎電圧源と電流源 ~等価電源と理想電源の違い
◎電圧源と電流源を含む回路の考え方
◎電圧源と電流源の接続方法の注意点
◎起電力と内部抵抗が等しい電圧源を複数並列に繋いだ場合の考え方
◎電力とジュールの法則
◎チップ抵抗器の定格電力と外形寸法表記
◎最大電力 ~最小定理の考え方
◎複数の電源から供給される電力の割合
