二分探索木C++

BSTは、ソートされたリストにデータを保持するデータ構造です。 これは、二分探索木として知られています。これは、ツリー内で、すべてのノードに最大2つの子があり、それ以上増やすことができないためです。 これは、存在するアイテムを検索または検索するために使用されるため、検索ツリーと呼ばれます。 この現象をC++言語で実装します。

実装

実装では、最初のステップは、整数型キーと左側ノードと右側ノードの両方を初期化するための構造を使用することです。 これらのノードは両方とも代替ノードのアドレスを保存するため、変数ポインターを使用して定義されます。 その後、構造を閉じます。

構造体を介して新しいノードを再度作成します。 関数のパラメーターには、ノードに入力するデータが含まれます。

struct node * newNode（int item）

データを格納する新しいノード一時を作成し、メモリのサイズはmalloc（）を介して割り当てられます。 ノードのキー部分にアイテム値を追加します。 一方、構造体で以前に宣言された左右の部分は、最初のノードであるため、現在はNullとして宣言されています。 臨時雇用者が返されます。

「inorder」という名前の関数が作成され、パラメーターのルートノードを受け入れます。 ご存知のように、ツリーには、ツリーのノード、左側、右側の3つの主要部分が含まれています。 ifステートメントを使用して、ルートがnullでないかどうかを確認します。 次に、関数を呼び出して、ルートの左側を送信します。 これにより、ツリー内のパスの方向を示す矢印が付いたルート自体が表示されます。 次に、右をトラバースするには、ルートの右をパラメーターとしてinorder関数を呼び出します。

順序（ルート->左）

これは、順序のトラバースが行われる方法です。 ツリーに新しいノードを挿入するには、ノードとキーをパラメーター値として受け取る関数を使用します。 ツリーがすでに空の場合は、新しいノードが返されます。 2番目のケースでは、ツリーが空でない場合は、最初に右側に移動して、ここに新しいノードを挿入します。 挿入には、if-elseステートメントを使用してキーの順序を確認します。 新しいキーは昇順で左側に移動します。 新しいキーをチェックする部分がノードにすでに存在する値よりも小さい場合は、ノードの左側にキーを入力します。

ノード–>左=挿入（ノード->左、キー）

一方、キーが大きい場合、それは正しい部分に移動します。

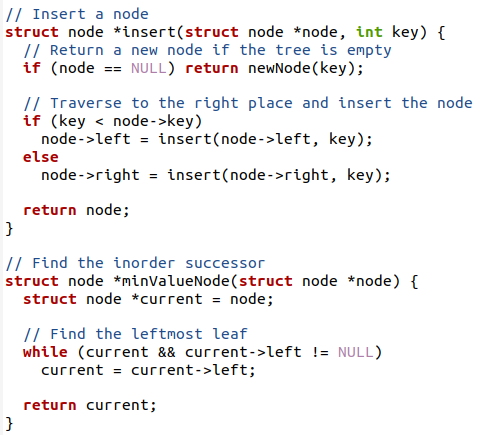
ノードの挿入後、次のノードまたは後続のノードをチェックします。 *currentという名前の新しいノードを作成するminvalueの関数が作成されます。 このノードは、関数に引数として渡される値によって割り当てられます。 最初に、ツリーの左側にあるコーナーノードまたは左側のモードリーフが見つかります。 ノードのトラバースが終了するまで繰り返すwhileループを使用します。 つまり、現在のノードの左側はnullではありません。

現在=現在–>左

左側のループ内で、現在のノードに次の現在の値を割り当て続けます。

私たちの木は、両側に葉を追加することによって横断され、整理されます。 各値は、メインプログラムからの関数呼び出しによって挿入されます。 ここで、任意の要素を検索する必要があり、見つかったら削除します。

C ++のツリーは、リンクリストと同じ現象で動作します。 ツリーに二分探索を適用し、削除操作を実行して、ツリーから1つのノードまたはリーフを削除します。 削除ノードの機能が作成されます。 ツリーと値がパラメータとして含まれます。 最初に、ツリーに値が含まれている必要があることを確認します。 したがって、ifステートメントが使用され、ルートがNULLの場合、ルートのみを返すことを意味します。

If（key key）

削除するキーがルートノードよりも小さいです。 次に、左側に移動し、ツリーの左側で削除関数を呼び出し、削除するキーを指定します。

ルート->左=deletenode（ルート->左、キー）;

そして、else-ifの部分についても同じことが言えます。 キーがノードキーより大きい場合は、正しいパスに移動し、削除関数を呼び出します。 ツリーの右側の部分とキーを渡して、削除するノードを簡単に見つけられるようにします。

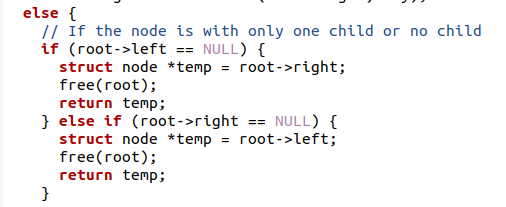
ここで、elseの部分に近づきます。これは、ノードが単独であるか、それ以上リーフがないか、または子が1つしかない場合に適用されます。 else部分の内部でも、右側にノードがないかどうかを確認するステートメントを使用する場合は、左側と同様に、ノードの右側の値を新しい一時ノードに追加します。

構造体ノード*temp= root-> left;

その状態で、ルートを解放します。 これにより、ルートから値が削除されます。

無料（ルート）;

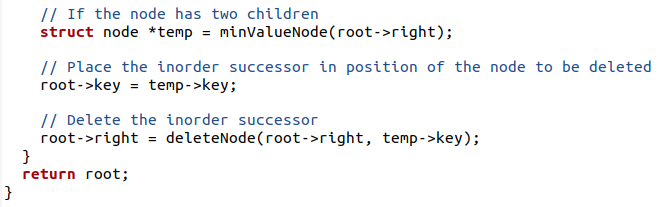
いずれかのノードに2つのリーフが含まれている場合、値を検索するには、最小値関数を使用し、右側の部分が関数に送信されます。

Minvaluenode（ルート->右）;

削除する値が見つかったら、ツリーの最後の部分として宣言して、簡単に削除できるようにします。

ルート->キー=一時->キー;

これを行った後、ノードを削除し、

ルート->右=ノードの削除（ノード–>右、一時->キー）;

関数を閉じた後、ここでメインプログラムを宣言します。 ルートノードは最初はNULLとして設定されます。 insert（）関数呼び出しを使用して、ノードへのルートと数値のデータを使用します。

挿入（ルート、5）;

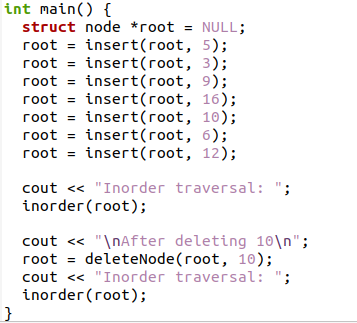
inorder関数は、ツリーの走査のために呼び出されます。

Inorder（root）;

次に、ノードを削除するために、削除関数を呼び出します。

ルート=deleteNode（ルート、10）;

削除後、値が再び表示されます。

コードを書いた後、コンパイラを介してUbuntuのターミナルで実行します。

ご覧のとおり、7つのアイテムがノードに入力されています。 1つが削除され、残りは以前と同じ順序で表示されます。

結論

二分探索木は、ソートされた形式で値を格納するために使用されます。 任意の番号を検索するには、すべての番号を最初に順番に並べ替える必要があります。 その後、ツリーを2つに分割してサブツリーを作成し、指定した数を検索します。 BSTの実装は、Ubuntuシステムで例を詳しく説明することによって行われます。 この記事がお役に立てば幸いです。 その他のヒントやチュートリアルについては、他のLinuxヒントの記事を確認してください。