今回は、「交流ブリッジ回路と平衡条件」についての説明です。
ブリッジ(橋渡し)している交流回路のこと。インピーダンスブリッジとも呼ぶ。交流ブリッジの平衡条件は、ブリッジの対辺インピーダンス値の積が同じになること。つまり、Z1Z4=Z2Z3の時に平衡になる。
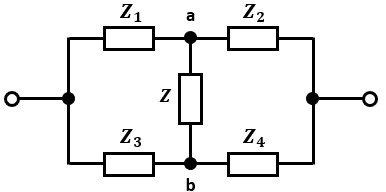
交流ブリッジ回路と平衡条件
詳しく説明していきますが、結論から言えば「直流ブリッジ回路」では抵抗によって構成されていた回路が、交流ブリッジ回路ではインピーダンスによって構成された回路に置き換わるだけです。
※ 説明には上のブリッジ回路の図1を用います。
交流ブリッジ回路はブリッジ(橋渡し)している交流回路のことで、図の端子a-b間が橋渡し部に該当します。
交流ブリッジが平衡すると、a-b間の電位差が0[V]となり、a-b間の回路には電流が流れなくなる、つまり開放されているものとみなすことができます。
ブリッジ部分を開放すると回路が簡略化できる為、ブリッジ回路の平衡条件は知っておくと便利です。
交流ブリッジ回路の平衡条件は、ブリッジの対辺インピーダンスの積が同じになることです。
対辺インピーダンスとは、ブリッジしているインピーダンスZを基準にして、対角線上に位置するインピーダンスを指します。
つまり、Z1Z4=Z2Z3の時に平衡になります。
平衡条件の求め方については簡単にしか触れません。
気になる方は練習だと思って計算してみましょう。
Z1の両端の電圧=Z3の両端の電圧、Z2の両端の電圧=Z4の両端の電圧になれば、a-b間の電位差は0[V]となり、a-b間の回路に電流が流れなくなるなるので、回路は平衡します。
この関係を整理するとZ1Z4=Z2Z3が導き出せます。
練習問題を1問用意しましたので、実際に数値を当て嵌めて考えてみましょう。
・以下の交流ブリッジ回路が平衡している時、LをCを用いて表しなさい。
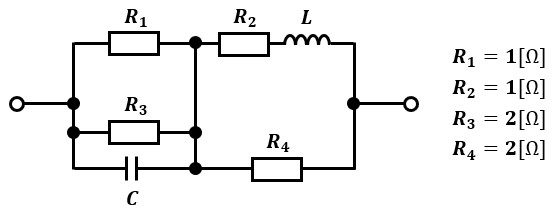
交流ブリッジ回路が平衡している時、ブリッジの対辺インピーダンスの積が等しくなります。
なので、まずは各インピーダンスの値を求めましょう。
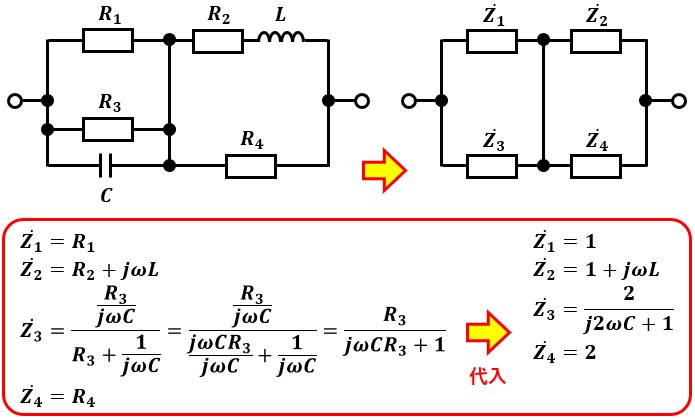
インピーダンスで構成された回路の形にできたので、Z1Z4=Z2Z3を計算します。
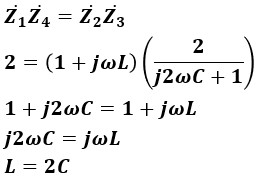
以上より、答えはL=2Cとなります。
以上、「交流ブリッジ回路と平衡条件」についての説明でした。
【基礎から学ぶ交流回路】
◎直流と交流の違い ~極性が変わらなければ交流ではない
◎正弦波交流 ~正弦波の周期と周波数
◎正弦波交流の位相のズレ
◎正弦波交流の平均値と実効値
◎交流電圧の平均値の求め方 ~正弦波編
◎交流電圧の実効値の求め方 ~正弦波編
◎交流電圧の平均値の求め方 ~三角波編
◎交流電圧の実効値の求め方 ~三角波編
◎整流形計器の平均値と実効値
◎正弦波交流のベクトル表示・フェザー表示
◎交流回路のオームの法則
◎交流電流の位相の変化 ~リアクタンス成分は位相がπ/2ズレる
◎R-L-C直列回路のポイント ~インピーダンスの三角形を描け!
◎R-L-C並列回路のポイント ~電流の三角形を描け!
◎交流回路の共振 ~直列共振と並列共振について
◎R-L-C直並列回路の共振
◎交流回路の電力 ~位相差による力率という考え方
◎交流回路のインピーダンスと電力の関係
◎交流回路のインピーダンスの複素数表示
◎交流回路の電力の複素数表示
◎交流ブリッジ回路と平衡条件
◎過渡現象と時定数
◎R-L-C直並列回路の定常状態の考え方
◎ひずみ波 ~基本波・高調波とは?
◎ひずみ波の消費電力 ~抵抗で消費される平均電力の求め方
◎変調 ~ひずみ波の使われ方とAM変調度の求め方
◎復調 ~ひずみ波から特定の周波数を取り出す方法
